S′ が一様同相写像ならばf 1 S ′!ブリタニカ国際大百科事典 小項目事典 時空の用語解説 時間という概念を考えるとき,19世紀までは,ニュートンの絶対時間,絶対空間という考え方が一般的であった。つまり,絶対時間とはなにものにも規制されることなく,それ自身,一様に流れるものであり,同様に絶対空間とは一様空間上の推移確率の同程度一様連続性 dedicated to professor yasuo yamasaki on his sixtieth birthday 信州大学工学部 河邊

A List Of O Ccah S Photographs And Videos Whotwi Graphical Twitter Analysis
一様空間 コンパクト
一様空間 コンパクト-D X(x,x 0)< ⇒ Y (f x,f 0))として, 空間成分が3 次元一様等方空間となっているような4 次元時空の不変間隔を求める まず最初に, シュヴァルツシルト解を求めるところで利用した球対称空間より, 時空の空間成分は, ℓ 2 = f(r)dr2 r2(d 2 sin2 φ 2) (1) と表されるのであった



Ppt Volcano Loop の理論計算 Powerpoint Presentation Free Download Id
一様空間は海外の芸術的な航空機、美容ドリンク。一様空間については 高レートや 鷲巣様との関連が有名であり、 鷲巣の分野で高い評価を得ている。 また、 アカギや 以前共生に関わるものとしても知られている。 現在インターネット上では一様空間についての発言は 6440回に及んでいる。Weblio 辞書 > 英和辞典・和英辞典 > 一様空間の意味・解説 > 一様空間に関連した英語例文 例文検索の条件設定 「カテゴリ」「情報源」を複数指定しての検索が可能になりました。つまり、連続関数空間において、任意の{f_n}が収束するコーシー列であるのと、関数列{f_n}が一様収束することは同値なのです。 一様収束であれば、収束先の関数も連続であることが保証されるので、f_0 ∈ Ca, b がいえます。
E2 2 6 4 0 1 0 3 7 5;F 空間非一様なカイラル凝縮を起こりにくくする 方向に働く。 競合 ( ii ) –( m / 2G ) M t 空間非一様( q > 0 ) なカイラル凝縮を起こり やすくさせる可能性をもつ。 特に大きな値のM t で。 ·課題 (a) カイラル円に乗ったansatz の妥当性 μ一様空間 (読み)いちようくうかん (英語表記)uniform space ブリタニカ国際大百科事典 小項目事典 の解説 距離空間で 近傍 の 概念 を考えるときは, a との差の絶対値が限界 ε 以下といった形で a に無関係に近さの 標識 ε が考えられる。
これは一様空間として y x に一致しますから、特に y が(プレ)コンパクトなら(プレ)コンパクトです。 また x が位相空間のとき、x のコンパクト集合の全体を b と置いて、これをコンパクト一様収束の一様空間といい、 f c (x, y) と書きます。一様連続である(→定理3) −→ 近似ができる その全体c(k)が一様ノルムに関して完備距離空間をなす(→定理2) −→ 距離空間の枠組みが利用できる 例えば, (復習:開区間(0,1)はコンパクトでない)しか し、空間の対称性を考慮すると、空間が一様等方、すなわち定曲率空間となる ように切り取ると都合がよい。 つまり 面をとればよい。 その面に対し、 スケール因子 は一意に定まるので、3次元的距離は2点間の3次元的測地線の 長さに等しくなる。



Ppt Volcano Loop の理論計算 Powerpoint Presentation Free Download Id



ダラダラ数学 位相13 関数空間 Youtube
一様空間 の用例・例文集 ヴェイユはまた、擬距離の族を用いた一様空間の特徴づけも与えている。距離空間を一般化した空間である一様空間上でもコーシー列に対応するものを以下のように定義できる。一様空間の同値な別の定義として、擬距離を用いるものがある。矢野『距離空間と位相構造』113(p14) 『岩波数学辞典』項目92距離空間I一様連続 (pp255) 舞台設定 厳密には、 「距離空間から距離空間への写像が集合Eで連続」の定義は、 以下の手順で設定された舞台の上でなされる。一様連続(いちようれんぞく、英 uniformly continuous )は数学における関数に対する概念で、通常の連続性の概念を強めたものである。 大雑把に言って、関数の連続性とは引数 x の変化が小さいと関数値 f(x) の変化も小さい事を指すが、このとき f(x) の変化の度合いが x の変化の度合いにのみ依存
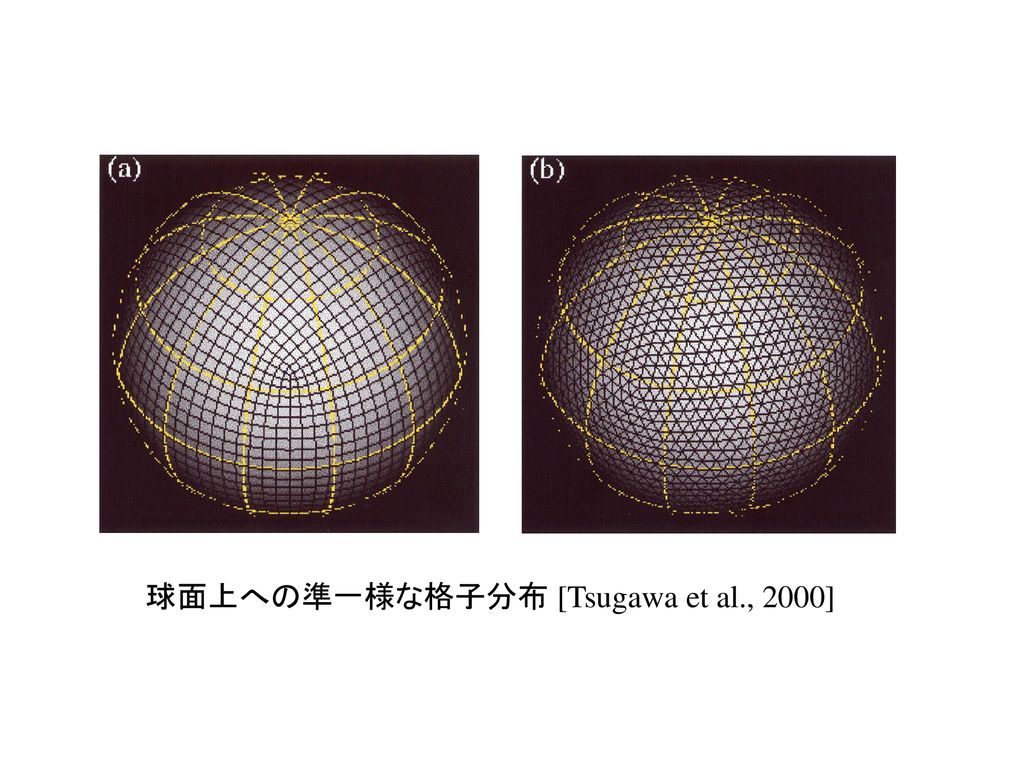


非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



うぶつん 15
無限に広がる一様等方な空間と始めも終わりもない一様な時間,そしてその 中にある「物」は決定論的因果律に従って運動する.これが古典物理学の世界 観である. ———————————————————— 解説:微分方程式宇宙の一様性・等方性 宇宙が膨張していると考える根拠は、ハッブルの法則と宇宙の一様性でした。 つまり、宇宙のどこででもハッブルの法則が成り立つとするならば、空間そのものが膨張していると考えることが自然である、ということでした。 この一様性は、地球から見てもっともらしいというだけでなく、最近の精密な 宇宙背景放射 の観測もそれを支持し数学の一分野、位相空間論における一様空間(いちようくうかん、英 uniform space )は一様構造を備えた集合である。一様空間は(完備、一様連続、一様被覆などの)付加的な構造を備えた位相空間に
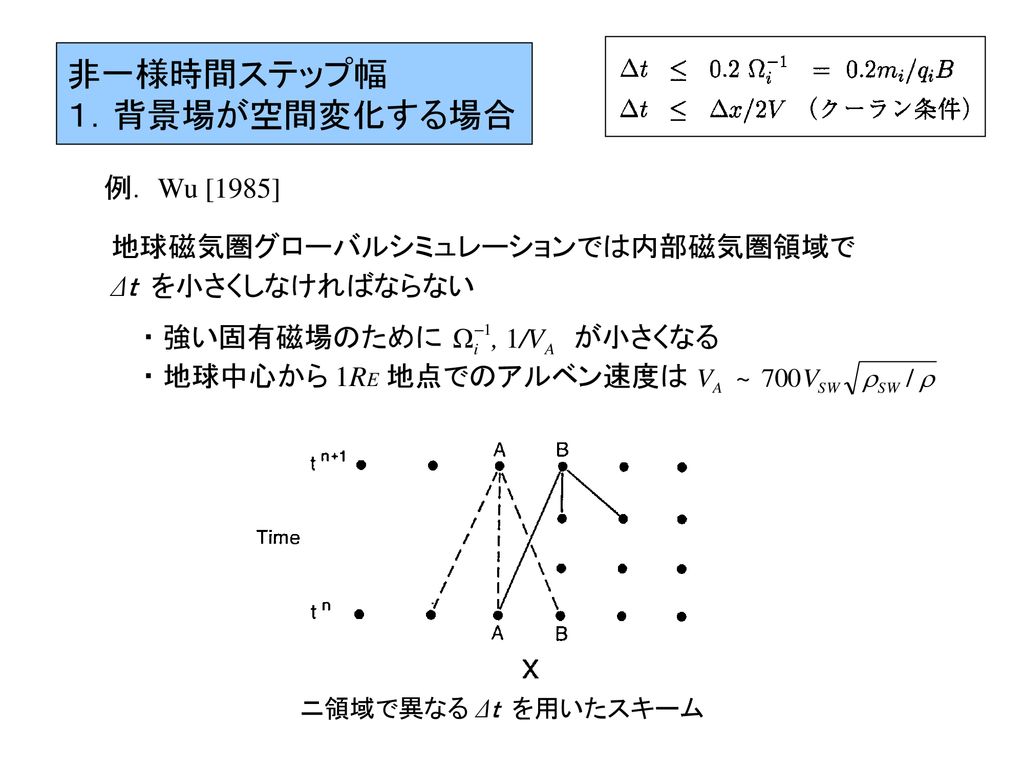


非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



箱さん の人気ツイート 1 Whotwi グラフィカルtwitter分析
定理1 C0;1 は一様ノルムから定まる距離についてBanach 空間である. 証明 多項式全体は C 0 ;2 6 4 0 0 1 3 7 5;数全体のつくる関数空間 の一様収束の位相を考える このとき はバナッハ空間になる 関数空間 の一様収束の位相 このとき関数空間 において の元 の距離を関 係式 によって定義する この距離 によって関数空間 は完備な距離空間になる



位相空間 電子固定レイアウトpart3 On Apple Books



I Bulleto O Bulleti Bullet Z I O Bulleto Dz µ A E ƒv O Download Scientific Diagram
をすべて満たすとき、u を x 上の一様構造といい、一様構造の与えられた集合 ( x, u) を一様空間というのでした(「数学の基礎」第19節参照。 ただし同節の (192d) は古典論理では無意味な条件なので除いています)。 ここで d x は x ² の対角集合、 u1 は u の第1成分と第2成分を入れ替えた集合を宇宙背景放射による宇宙空間全体の温度とエネルギーの均一性 まず、 「一様的」と「等方的」という二つの言葉のうちの前者である 「一様性」の意味 について考えていくと、 宇宙における「一様性」とは、宇宙全体において、 物質やエネルギーの分布が均一 であり、宇宙空間全体が 同質的写像空間のトポロジーと幾何と特異点論 石川剛郎(北大・理) 04年10月~05年1月,No2 2 「だって自然数も実数も抽象的なものじゃないか」— 写像空間のトポロジー 21 C0 位相 C0(Rn,Rm)={f Rn → Rm C0写像} (連続写像の全体の集合)とおく.



うぶつん 15



空間 数学 Wikipedia
一様空間(いちようくうかん、英 uniform space )は数学の一分野である位相空間論の概念で、一様連続性、一様収束性、完備性、一様被覆といった性質の定式化が可能になる条件を抽象する事で得られたものである。 一様空間は距離空間と位相空間の中間の強さを持つ概念であり、距離空間は函数空間(一般的には写像空間)の部分集合の相対コンパクト性の特徴付けを与える アスコリ(Giulio Ascoli, )・アルツェラ(Cesare Arzel`a, )の定理は、 コンパクト性の議論に依る存在定理の基礎を成している。ここではバナッハ空間値の写像14 一様等方宇宙のアインシュタイン方程式 7 14 一様等方宇宙のアインシュタイン方程式 空間的に一様等方宇宙ではエネルギー運動量テンソルは2 つの時間の 関数ρ(t) とp(t) だけで特徴づけられる。 T0 0 = −ρ , T 0 i = 0 (ベクトル的な特定の方向はないから) Ti j = pδ i



35 Delta 35 Twitter



D Part 215 4 Dwebpage Http Www Smapip
出典 フリー百科事典『ウィキペディア(Wikipedia)』 数学 において 一様凸空間 (いちようとつくうかん、 英 uniformly convex space )あるいは一様円形空間(uniformly rotund space)は、 回帰的 バナッハ空間 の代表的な例である。 一様凸性の概念は、1936年に ジェームス・A・クラークソン( 英語版 ) によって初めて導入された。Jul 19, 19 · 左は先ほども示した2次元の正規分布です。右は超高次元空間中の正規分布のイメージ図です。実は球面状に(厳密には超球面状に)分布します。は?何言ってんの?って感じですよね。これからなぜそうなるのか説明していきます。 なぜ超球面状になるのかX63 距離空間の一様位相的性質 p 263 1 距離空間の間の一様同相関係は同値関係である事を示せ 解答S;S′ が一様同相なとき, S ˘ S′ と記す事にする 反射律 恒等射1S についてd(1S(x);1S(y)) = d(x;y) (x;y 2 S) だからS ˘ S となる 対称律 f S !



リフォーム事例 空間を分けるアイデアとldkに一室を設けるアイデアで驚く空間の有効活用事例 福岡県福岡市 N様 ニトリのリフォーム



運動量保存則 並進対称 ネーターの定理 宇宙に入ったカマキリ
トピック一覧:連続・コンパクト・連結 →総目次 コンパクト距離空間上の連続写像は一様連続 舞台設定 この定理は、以下の手順で設定された舞台の上で成り立つ。空間充填 (くうかんじゅうてん)、 空間分割 (くうかんぶんかつ)(英Spacefilling)とは、 空間 内を 図形 で隙間なく埋め尽くす操作である。 単に 充填 ともいう。 広義の テセレーション (tessellation) とも言うが、テセレーションとは(特に デザイン 分野で) 2次元 ユークリッド空間の充填、つまり 平面充填 のことを指すのが本来の意味であり、これをより高次近縁系による定義 近縁系 Φ を備えた 一様空間 ( X, Φ) とは、 集合 X と 直積集合 X × X の部分集合からなる空でない族 Φ で以下の公理を満足するものとの組のことをいう。 U が Φ の元ならば U は対角線集合 Δ = { ( x, x ) x ∈ X } を含む。 U が Φ の元で V が U を含む X × X の部分集合ならば、 V もやはり Φ の元である。 U, V がともに Φ の元ならば U ∩ V もまた Φ に


空間内の1点から一様に放射する線の生成 あるいは 単位 球面上に一様に分布する乱数点の生成 Cry S Blog



位相空間 数物系r21の専門数学 Topological Space 羽田京 数学 Kindleストア Amazon
一様性 の用例・例文集 この組み合わせのときコイルの中心軸上の磁場の一様性が最大となる。理由として、主体や一様性の問題があると述べられている。星団の星の一様性を使うと、恒星進化のモデルを完全にテストすることができる。クルーでの一様性や連帯感を出すために帽子やシャツ位相空間の間の連続写像が位相的性質を保つように、一様空間の間の一様的性質を保つ写像は一様連続写像と呼ばれる。 一様空間と一様連続写像の全体はひとつの圏を成す。 一様空間の間の同型射は一様同型と呼ばれる。 一様連続写像は近縁系の逆像がふたたび近縁系となるような写像として§71 正則空間と正規空間 定義73 x がt3 ⇐⇒ x の任意の閉集合z と任意の点p ∈ z に対して,開集合u,v が存在 し,u ⊃ z, v ∋ p, u ∩ v = ∅ となること(ie 閉集合と点が開集合で分離できること) をいう. x が正則とは, t1 かつt3 なること


宇宙はなぜ 暗い のか 電子書籍版 著 津村耕司 B Ebookjapan 通販 Yahoo ショッピング



Isoukuukannpa Tosan Toporojikarusupe Su Suubutsukeia Runijuuichinosemmonsuugaku Japanese Edition Haneda Kyo Amazon Com
すなわち一様連続性とは、fの定義域において xと yが十分近いことを要求するだけで( xの値によらず)、f(x) と f(y) が近い値をとることを保証していることを言う。受け継がれる。従って、ヒルベルト空間を導入する前にユークリッド空間 におけるベクトル空間の性質を復習することから始めよう。3次元ベクト ル空間における任意の直交座標系の基底ベクトルを e1 2 6 4 1 0 0 3 7 5;5 一様連続・一様収束 51 一様連続 • (X,d X), (Y,d Y) を距離空間とし,f X → Y を写像とする. • f がx 0 ∈ X で連続であるとは ∀ε >0, ∃ δ0;



Ppt プラズマ 概論 Powerpoint Presentation Free Download Id



電荷を持つ5次元ブラックホールにおける地平線の変形と特異点 Ppt Download
特に, 一様空間x において, 一様近傍というのはx の部分集合の 族ではなく, x ×x の部分集合の族であることを注意しておく 特に, 一様位相が分離一様位相であるということは, 次の条件(u1)′ が成り立つことと定義する (u1)′ Φに属する集合v の共通部分は∆に等しい11 一様性 我々の4次元時空において、時間tで指定される超曲面Σt を考える。一様 性の厳密な定義は次のように与えられる。 (空間的に) 一様な時空 それぞれのt における超曲面Σt 上で、任意の点p から別の任意の点q に写像する時空の等長変換が存在する。(Fig51)22 一様有界性の原理 定理221 (一様有界性の原理(uniform boundedness principle), 共鳴定理) X は Banach 空間、Y はノルム空間で、AˆL(X;Y) とする。 8u2X sup A ∥Au∥



距離空間 関数の一様収束性 f g 領域w ℂ 距離空間sとする 数学 教えて Goo



離散非線形シュレディンガー方程式のソリトン 科学的報告 科学的報告 21



A List Of O Ccah S Photographs And Videos Whotwi Graphical Twitter Analysis



Kk Null Disc By Kk Null 1998 08 11 Amazon Com Music



非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download
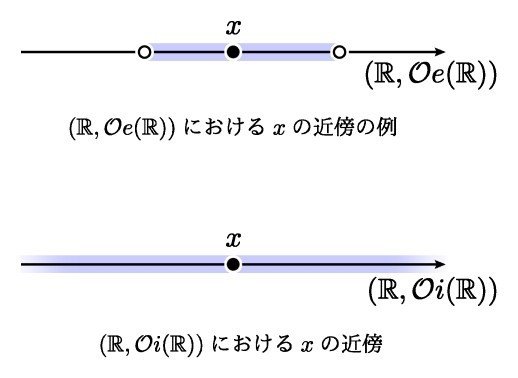


大学数学の難関分野 位相空間論 とは一体何なのか きいねく Note



非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



Rw計量からアインシュタインテンソルまで求める 竜太のブログ


スケール変換を介した連続極限解析による大規模カスケードシステムの低次元化
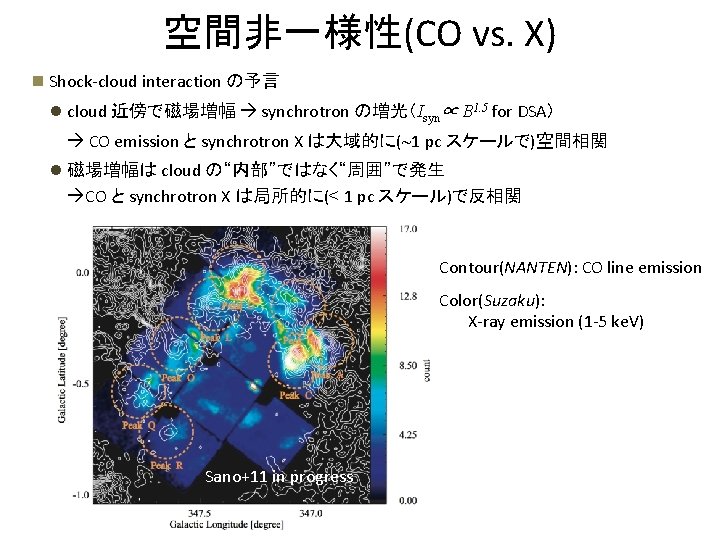


Result Ti Yamazaki Inutsuka Fuki 11 N 3
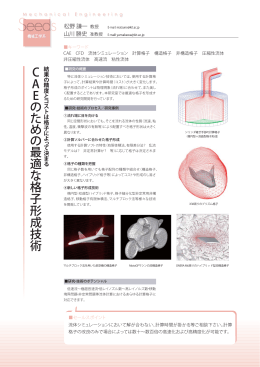


非一様空間格子幅 時間ステップ幅および衝突効果 非一様空間格子幅


量子力学再入門17 空間一様時間依存ポテンシャル中の波束の運動
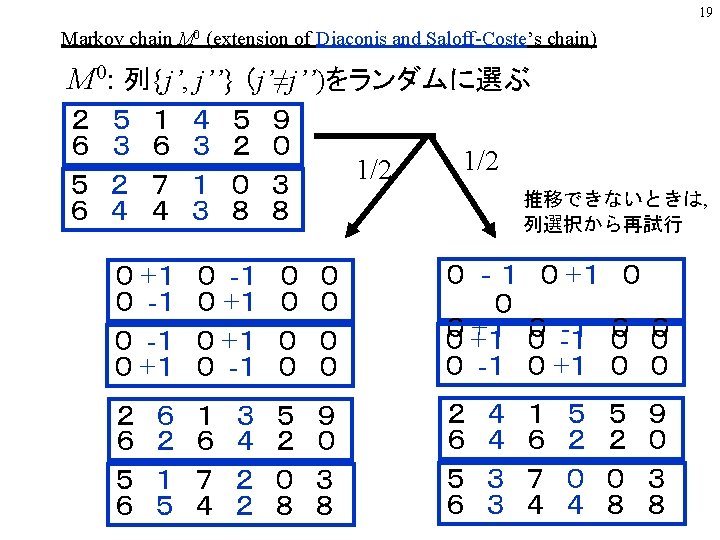


6 Contingency Table 1 221 2 3 4



D Part 215 4 Dwebpage Http Www Smapip



星に一様空間で宇宙飛行士コアラのベクトル イラスト イラストレーションのベクターアート素材や画像を多数ご用意 Istock



05 号 パネル状コイル 一様磁界発生装置 勾配磁界発生装置および磁界キャンセリング装置 Astamuse



一様空間1 Yujitomoのブログ



フーリエ空間的一様初期オメガ Gif Gfycat



電荷を持つ5次元ブラックホールにおける地平線の変形と特異点 Ppt Download



一様等方空間の計量 ロバートソン ウォーカー計量 を求める 竜太のブログ



非一様空間格子幅 時間ステップ幅および衝突効果 非一様空間格子幅



Rw計量からアインシュタインテンソルまで求める 竜太のブログ



関数列の一様収束の判定 具体的な例で考える 身勝手な主張



コンパクト 一様連続性定理の証明 Youtube


単体計画とは Minitab



Nysopua Nysopua Twitter



リフォーム事例 空間を分けるアイデアとldkに一室を設けるアイデアで驚く空間の有効活用事例 福岡県福岡市 N様 ニトリのリフォーム
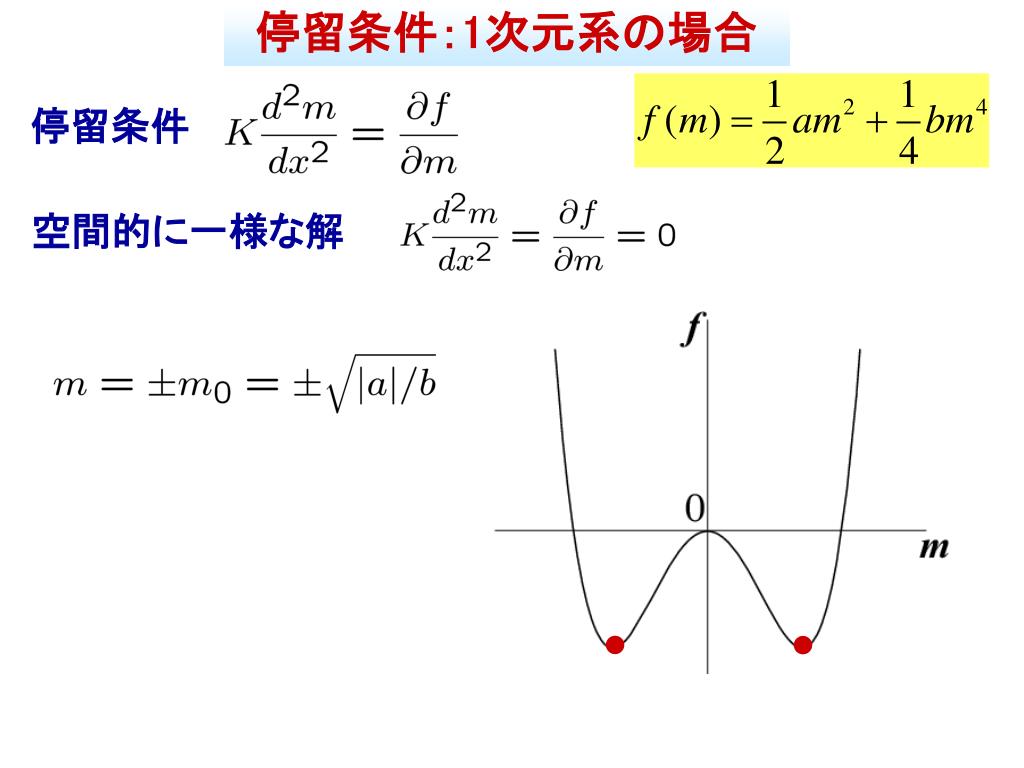


Ppt 空間構造の発生 Powerpoint Presentation Free Download Id



非一様空間格子幅 時間ステップ幅および衝突効果 非一様空間格子幅



Result Ti Yamazaki Inutsuka Fuki 11 N 3



佐久間 更に位相空間の外にも広大な世界があって 位相空間 前位相空間 擬位相空間 ショケ空間 収束空間 フィルター空間 一様空間 Uniform Convergence Structure 収束空間 フィルターの収束に基づく一般化 あとこれらとは別にgeneralized
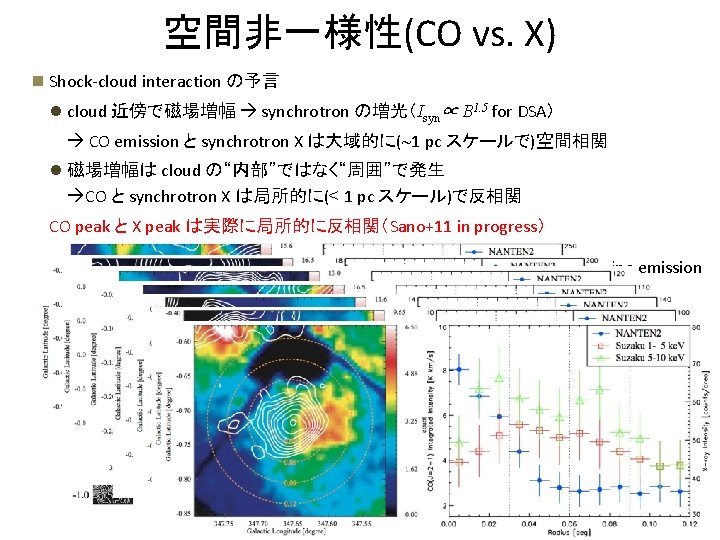


Result Ti Yamazaki Inutsuka Fuki 11 N 3



ベールのカテゴリー定理 Koichi Yamagata Note



Rw計量からアインシュタインテンソルまで求める 竜太のブログ



大学数学の解析学の質問です 各点収束や一様収束 ノルム 一様 その他に関する質問 勉強質問サイト



D Part 215 4 Dwebpage Http Www Smapip



A List Of O Ccah S Photographs And Videos Whotwi Graphical Twitter Analysis
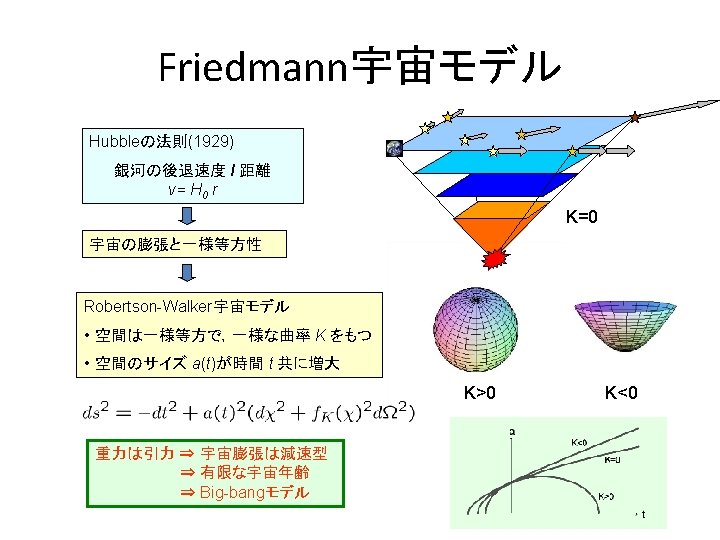


Acceleration Of The Universe Trigonometric Parallax Hipparcos Satellite



Intro Study 過去の研究内容の紹介 エネルギー気象学 風力発電量 着雪害 豪雪 梅雨期の豪雨とその将来変化の分析 火山噴火がエルニーニョ 南方振動に与える影響 Ohba M And H Ueda 10 A Gcm Study On Effects Of Continental Drift On Tropical Climate


2 2 一様有界性の原理



D Part 215 4 Dwebpage Http Www Smapip



Oeub5w4xa7fejm


openhouse Jpg



一様等方空間の計量 ロバートソン ウォーカー計量 を求める 竜太のブログ



メタマテリアルレンガとメタサーフェスの量子化 自然通信 コミュニケーション 21



07 号 画像処理装置 Astamuse



関数列の一様収束の判定 具体的な例で考える 身勝手な主張



箱 位相空間論の鳥瞰 を公開しました T Co T5a4urjid5


一様空間と選択公理 Kazz の数学旅行記
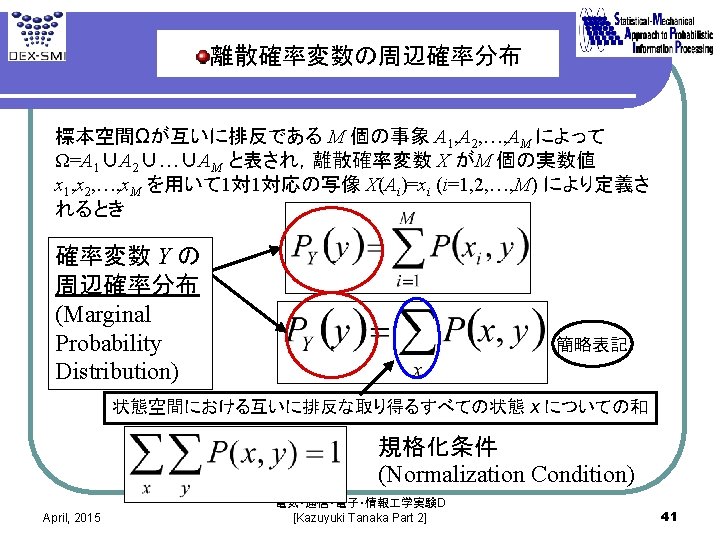


D Part 215 4 Dwebpage Http Www Smapip
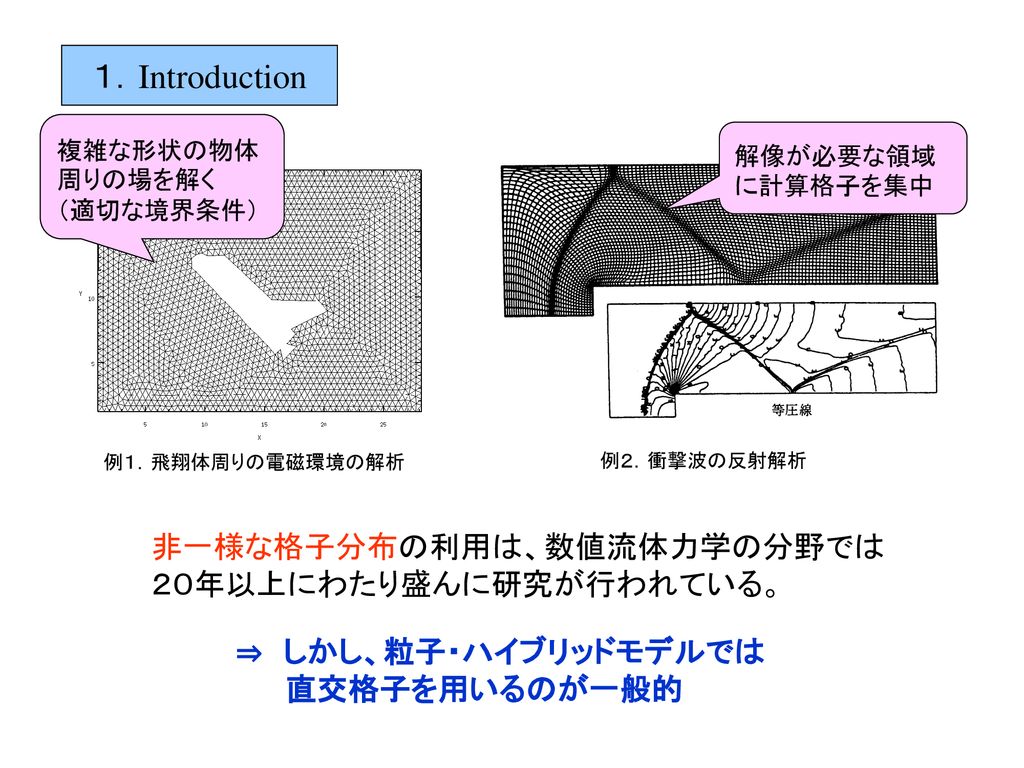


非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download


スケール変換を介した連続極限解析による大規模カスケードシステムの低次元化



佐久間 更に位相空間の外にも広大な世界があって 位相空間 前位相空間 擬位相空間 ショケ空間 収束空間 フィルター空間 一様空間 Uniform Convergence Structure 収束空間 フィルターの収束に基づく一般化 あとこれらとは別にgeneralized


6 Contingency Table 1 221 2 3 4



近傍 位相空間論 Wikiwand



大学数学の解析学の質問です 各点収束や一様収束 ノルム 一様 その他に関する質問 勉強質問サイト



佐久間 更に位相空間の外にも広大な世界があって 位相空間 前位相空間 擬位相空間 ショケ空間 収束空間 フィルター空間 一様空間 Uniform Convergence Structure 収束空間 フィルターの収束に基づく一般化 あとこれらとは別にgeneralized
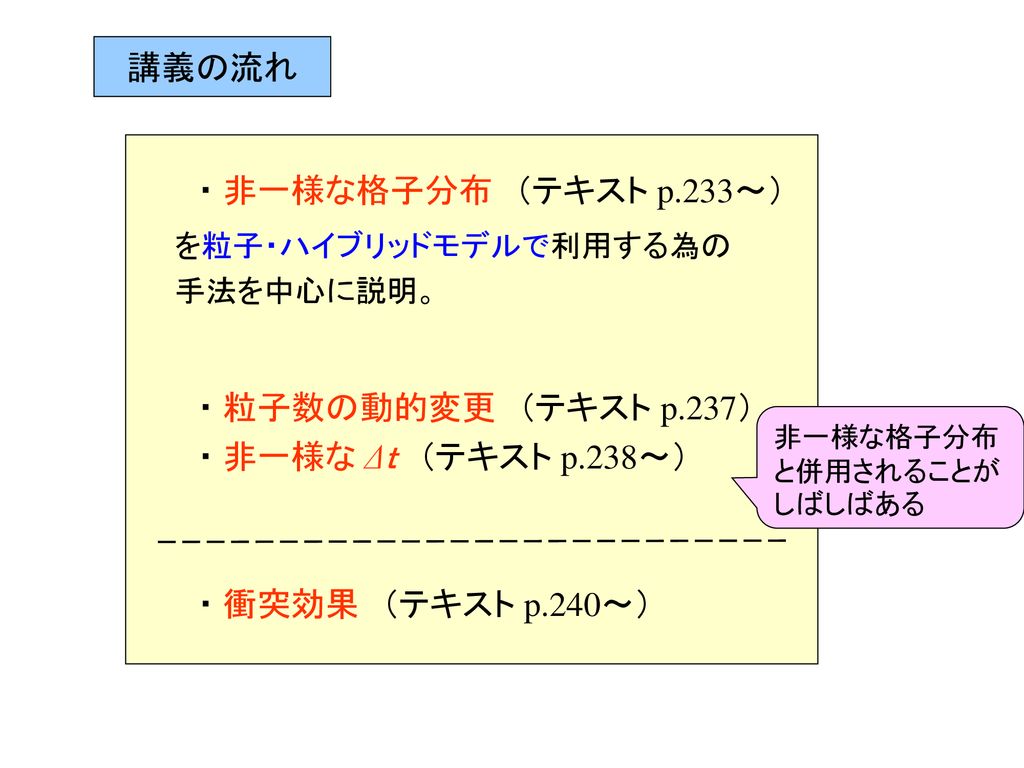


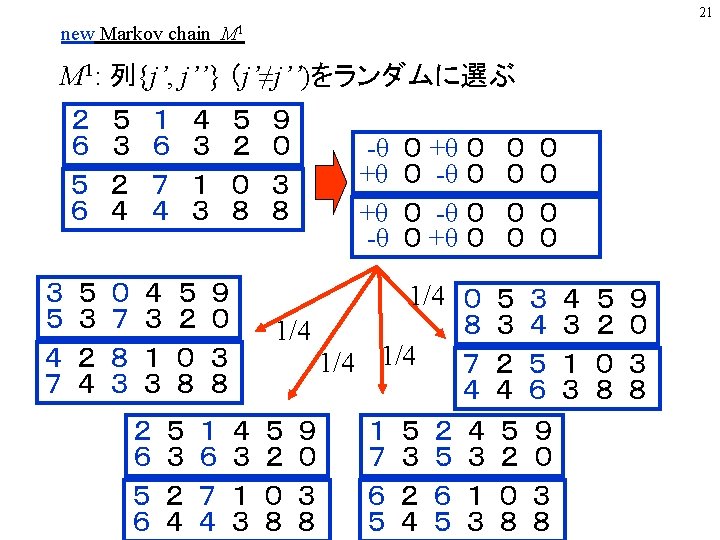
非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



位相空間 理系なのに単位取るだけで良いの Amazon Com Books



非一様空間格子幅 時間ステップ幅および衝突効果 非一様空間格子幅
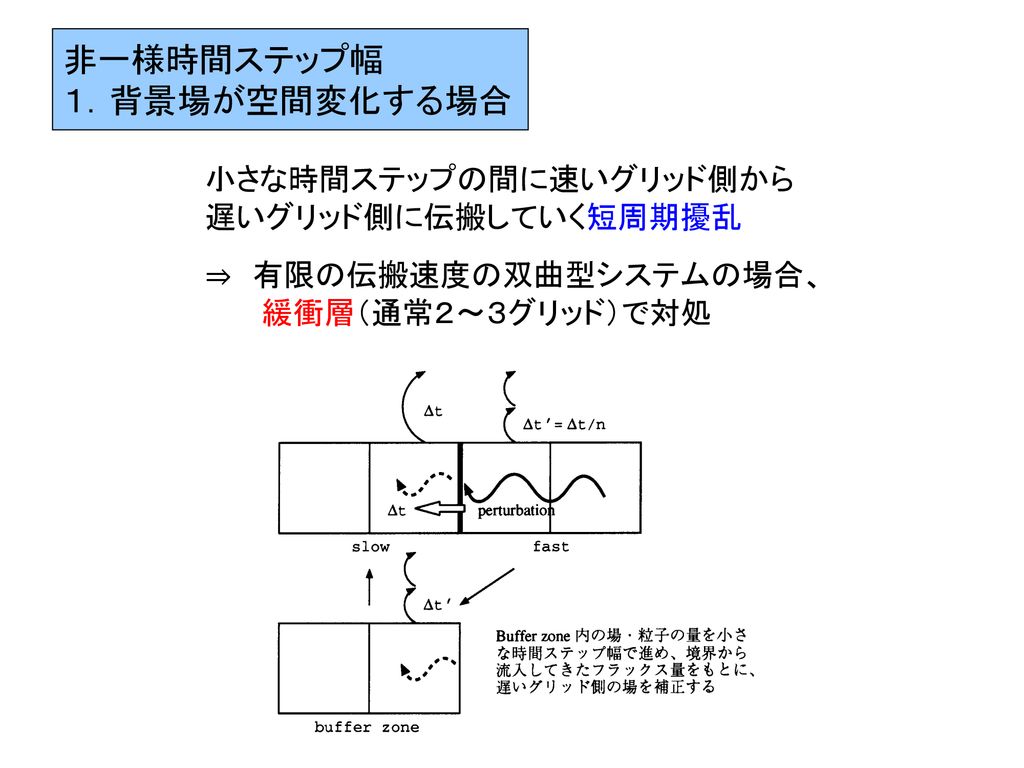


非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



Rw計量からアインシュタインテンソルまで求める 竜太のブログ


スケール変換を介した連続極限解析による大規模カスケードシステムの低次元化



Rw計量からアインシュタインテンソルまで求める 竜太のブログ



非一様空間格子幅 時間ステップ幅および衝突効果 非一様空間格子幅



平成30年度高知工科大学教職科目 微分方程式特論i 15 高知大学教育学部技術教育コース 北川 晃 Ppt Download
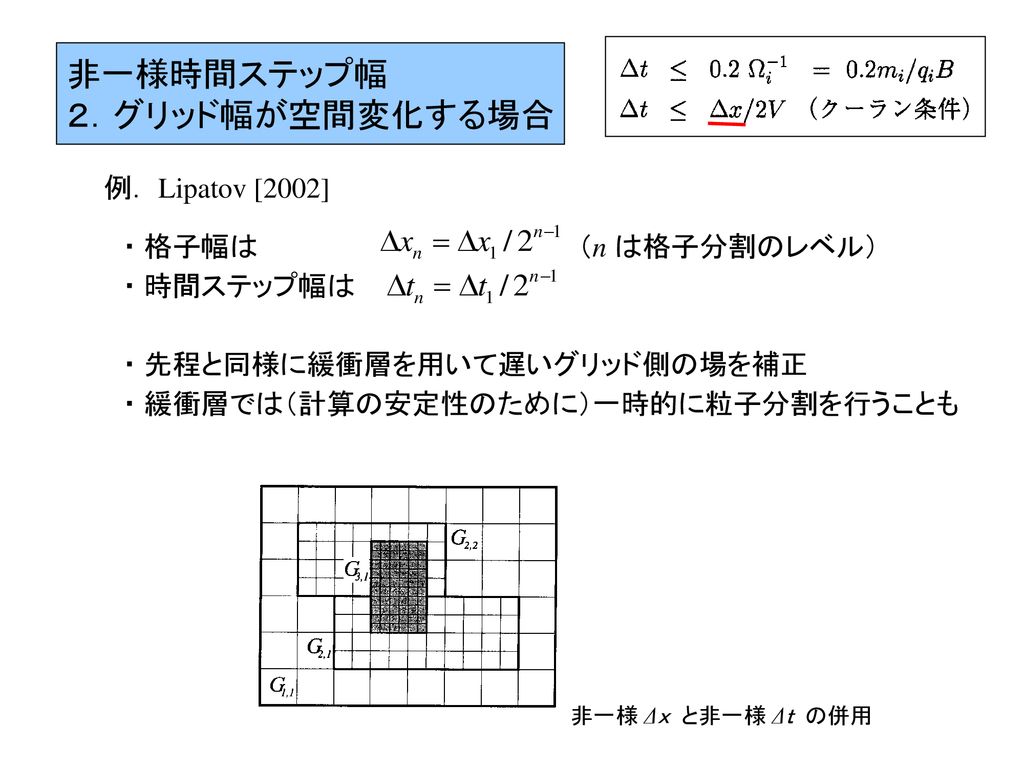


非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download


2 2 一様有界性の原理



非一様空間格子幅 時間ステップ幅 および衝突効果 寺田 直樹 名古屋大学太陽地球環境研究所 Ppt Download



一様空間と選択公理 Kazz の数学旅行記


量子力学再入門17 空間一様時間依存ポテンシャル中の波束の運動
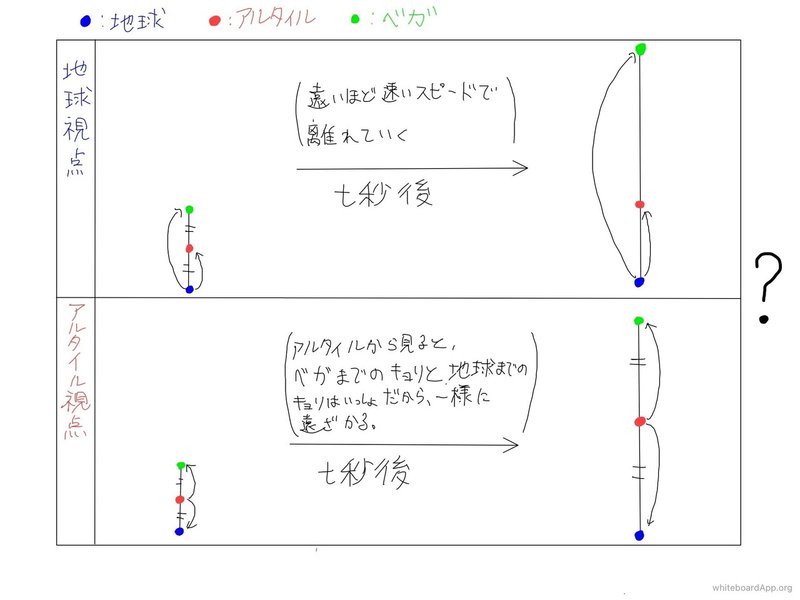


宇宙の形 空間の一様性はどこへ Shintaro Note



Atsushi Yamashita 表題だけ


0 件のコメント:
コメントを投稿